I recently came across an intriguing problem in calculus with real-world implications, and I thought it would be interesting to share it with you in a bit more detail. Lanchester’s Square Law involves a set of differential equations that model the relative strengths and interaction of two armies. Devised during WW1, it was used to illustrate power relationships and potential outcomes between opposing militaries.
The relationships demonstrated here have also been observed elsewhere. For example, researchers noticed that chimpanzees will typically follow the Lanchester’s Square Law before attacking a rival troop, reflecting that fact that they will weigh up and evaluate numerical advantages before acting.
In essence, the square law predicts that the fighting ability of a group is proportional to the square of the number of individuals, but rises linearly with the fighting prowess of individuals in each respective group. We will find the solutions to its most basic form, which can be used to predict the outcome of a battle of attrition involving two infantry forces. Under these assumptions, we can derive the following equations.

Here, x(t) and y(t) are defined to be the strength of two armies x and y, as a function of time. dx/dt is the rate of change in strength of army x, and dy/dt is the rate of change in strength of army y. The negative sign on the right-hand side reflects the fact that no reinforcements will support either army – in other words, the strengths/numbers of both armies will only decrease. Finally, a and b are both positive parameters which represent the rate at which each army destroys the other army, or their relative strengths. By common sense, we can deduce that if a = b, then both armies are of equal strengths, so the army which initially has more soldiers will win. On the other hand, if a >> b , then army y will win, as army x is wiped out at a much faster rate. But how can we characterise these outcomes numerically? To do this we must solve the system of differential equations.
Firstly, we note that we can characterise this system in matrix form, which provides a useful way to analyse its properties. Considering the coefficients of x and y, it can be depicted as follows.

This provides a way to utilise one of the most powerful tools in linear algebra; eigenvectors and eigenvalues, which dominate the characteristics of the system. We can solve for these and use them to characterise the general solution (with a few intermediate steps that I have omitted). Substituting initial conditions x(0) = x0 and y(0) = y0, which represent the intitial strength of armies x and y respectively, we can solve for the constants c1 and c2.


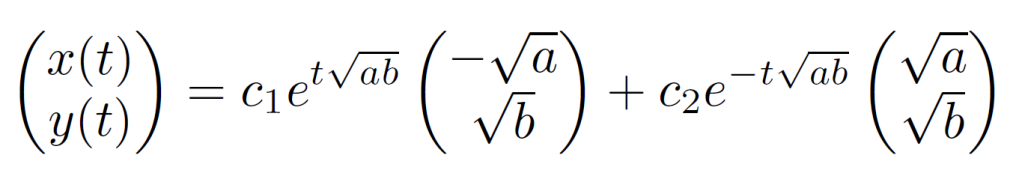
We can plot of all of the potential solutions of the system based upon the initial conditions, as depicted below. There is much to analyse here. Firstly, we describe this as a ‘saddle-point’. This is due to the behaviour of the eigenvectors and eigenvalues. Consider what will happen as an infinite amount of time elapses, and t -> infinity. Looking at the general solution, we can see that the term with the negative exponent is pulled down to zero in the limit. Overall however, the solution is dominated by the first term with a positive exponent.


It is apparent that this solution is parallel to the eigenvector v1, represented by the straight line from the top left quadrant to the bottom right quadrant in the plot. Notice that the arrows are pointing outwards – if we start on this line, as time increases, the solution diverges to infinity. On the other hand, if the initial condition is such that c1 = 0, then we are just left with the second term of the general solution with the negative exponent. As time increases, this term decreases in value, causing the solution to tend towards the origin. This is represented by the other straight line which passes through the top right quadrant, with arrows pointing towards the origin. We call this is sort of solution a ‘saddle’. The figure below illustrates why this is the case.
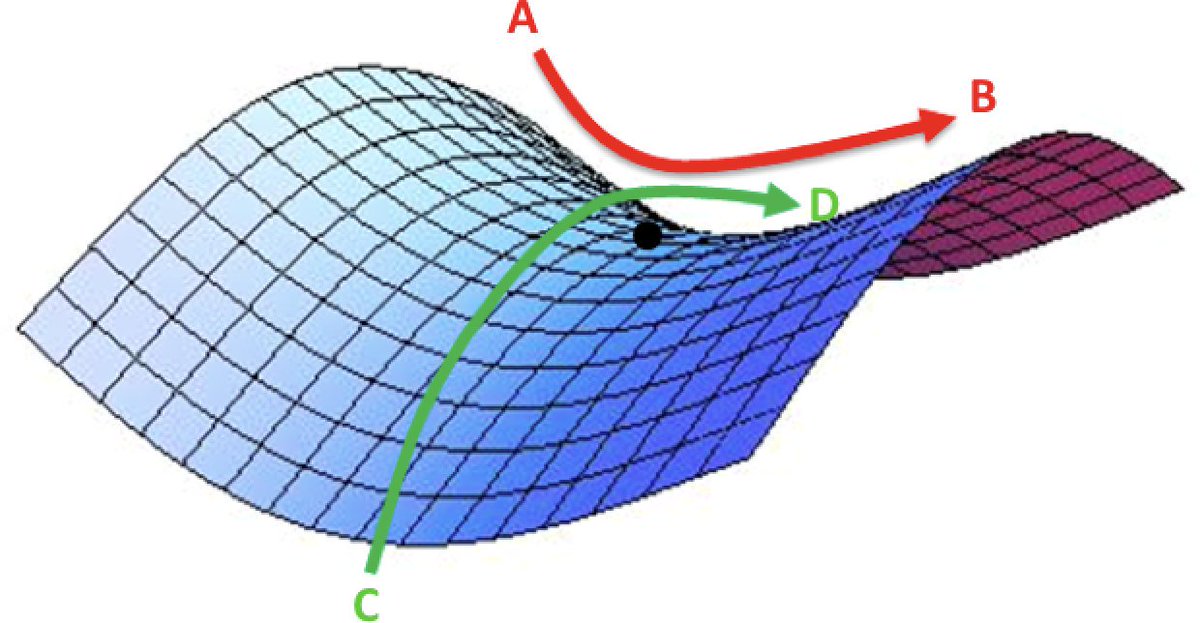
If a ball is placed at the centre of the saddle (the saddle point), and is pushed either to the left or right (in the direction C to D) , it will roll away, thus representing an unstable solution. However, if the ball is moved exactly parallel to the axis of the saddle (along the eigenvector v2, or along the line A to B), it will roll back to the saddle point – the solution is stable! The other curves on the graph are determined by these two eigenvectors. However, to better understand them we can explicitly compute y(x).

Which is a separable differential equation that can be solved by integrating both sides with respect to x.

Upon substitution of initial conditions, we can solve for the constant c.

This solution is characteristic of a hyperbola, exactly identical to the previous plot which we obtained by solving the system of differential equations using its eigenvectors. However, it is now a bit more obvious what will happen if we alter the initial conditions x0 and y0 and parameters a and b. Firstly it is important to note that negative values here do not make any sense – any army cannot have negative strength. Hence, we discard all but the positive top right quadrant. There are 3 cases to consider.
Case 1: If the following condition is met, y will defeat x in the long run.


Case 2: If the following condition is met, x will defeat y in the long run.


Case 3: If the following condition is met, y and x will wipe each other out in the long run.


I have also made an interactive plot using desmos which you can experiment with to see how the solution changes with different initial conditions and strength parameters.
https://www.desmos.com/calculator/9lukrs50jd
Increasing sophistication of the model and limitations
Whilst this is an interesting solution, the general characteristics can be deduced with common sense as we did earlier. Nevertheless, the Lanchester Square Law provides a strong foundation on which to build more sophisticated models. These may include variables such as army deployment, individual strengths, weaponry etc. A model can really be as complex as we desire. However, this raises the question, when do we stop, and how useful really are these models?
Indeed, in most cases empirical evidence does not clearly support the Square Law, and studies have yielded mixed results. In practice, it is impractical to rely on such a model to accurately determine the outcome of battles. Nevertheless, on a more macro level, it does provide a meaningful way to characterise the interactions between opposing forces. In my opinion, the fact that we have observed these patterns in nature is most revealing. When mathematics illuminates natural phenomena it reveals the fundamentals at play, and true beauty can be found in almost anything.
Bibliography

Fantastic article Dhruv. My initial fundamental knowledge of Saddle points has been strengthened! It is extremely interesting how Lanchester’s Square Law was devised during WW1. Clearly, a lot of thought and reasoning has ensued as this reasoning would have had a serious impact on the outcomes of the war. Personally, I believe that this law would have limited use in the current age due to Lanchester’s square law not taking into consideration technological force. Naturally, over time, technology has vastly improved and contributes a large amount towards a country’s military power. What are your thoughts on Lanchester’s Square Law in this day and age?
LikeLike
Hey Parth, thanks for your question. In practice, Lanchester’s Square Law really just provides a way to provide general insight into a simple battle. I can’t say that in itself it is particularly useful. However, this sort of modelling and way of thinking is the framework for much more complex analysis of military dynamics, which can play a meaningful role in wars.
LikeLike